某投资方案用于确定性分析的现金流量基本数据见表1-21,所采用的数据是根据未来最可能出的情况预测估算。由于对未来影响经济环境的某些因素把握不大，投资额、经营成本和产品价格均可能在土20%的范围内变动。设基准折现率i=10%。问题:1.试分别就上述三个不确定因素作单因素敏感性分析。2.考虑投资额和经营成本同时变动对项目净现值的影响，进行双因素敏感性分析。

问题1:

(1)设投资额为K，年营业收入为R，年经营成本为C，年增值税及附加为TA，期末残值为S，设投资额变动百分比为x；经营成本变动的百分比为y；产品变动的百分比为z。

进行确定性分析，计算净现值(NPV)的初始值:

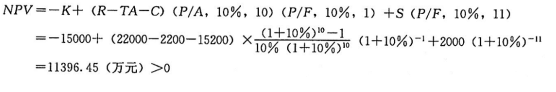
因此，方案在经济上是合理的。

(2)分析投资额、经营成本和产品价格变动对方案净现值影响，列出计算式:

NPV=-K(1+x)+(R-TA-C)(P/A,10%,10)(P/F,10%.1)+S(P/F,10%,11)

NPV=-K+[R-TA-C(1+y)](P/A,10%,10)(P/F,10%,1)+S(P/F,10%,11)

NPV=-K+[(R-TA)(1+z)-C](P/A,10%,10)(P/F,10%,1)+S(P/F,10%,11)

将表1-21中的数据代入上述三个公式，并分别取不同的z，y，z值，可以计算出各不确定因在不同变动率下的净现值。计算结果见表1—22。

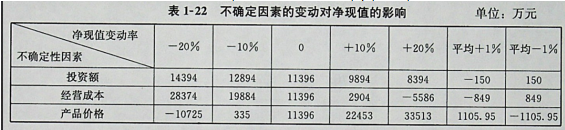
从表1-22中的数据分析可知，三个因素中产品价格的变动对净现值的影响最大，产品价格平变动1%，净现值平均变动1105.95万元；其次，是经营成本；投资额的变动对净现值的影响最小。

根据计算所得数据，绘出每个不确定因素的敏感趋势曲线，见图1-15、图1-16。

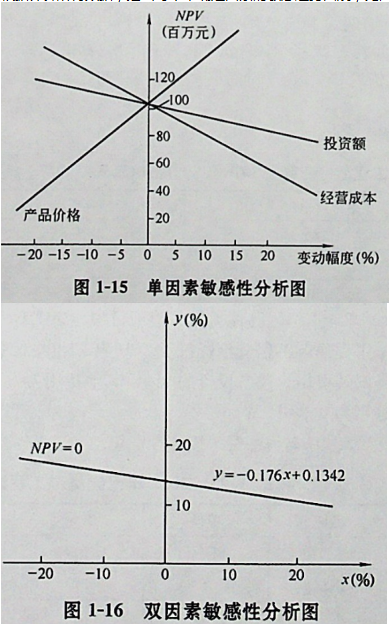
分别计算出当NPV=0时，x=76.0%，y=13.4%，z=-10.3%，即投资额与经营成本不变，产品价格低于预期值的10.3%以上；投资额与产品价格不变，经营成本高于预期值的13.4%以上，方案将变得不可接受。

问题2:

列出考虑投资额与经营成本两个因素的变动对净现值影响的计算公式:

NPV=-K(1+x)+[R-TA-C(1+y)](P/A,10%，10)(P/F,10%,1)+S(P/F,10%,11)

NPV=11396-15000x-84900y

取NPV的临界值，即令NPV=0，则NPV=11396-15000x-84900y=0

11396-15000x-84900y=0

y=-0.176x+0.1342

在x-y坐标系中作出上述直线，即NPV=0的临界线，见图1-16。陔直线将x-y平面分为个区域:在临界线左下方区域NPV>0;在临界线右上方区域NPV<0，投资额与经营成本同时变范围不超出临界线左下方的区域(包括临界线上的点)，方案都是可以接受的。