某保险公司为了更好地确定市场细分目标，需了解投保人的年龄睛况，据估计，40岁及以下的投保人占40%。为了验证该估计，公司随机抽取了36个客户的资料，得到他们的年龄隋况。经计算，得到40岁以下的投保人所占比率为41.67%。问：在显著性水平仅=0.05下，能否认为保险公司的估计是成立的？
参考答案： 首先，建立假设H0：π=40%，H1：π≠40%。
其次，选择统计量
，代入已知值可得：
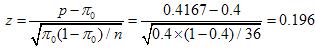
最后，因为是双侧检验，根据α=0.05，查正态分布表得临界值为：zα/2=z0.025=1.96。由于|z|=0.196＜za/2=1.96，因此不能拒绝原假设。在显著性水平α=0.05的条件下，说明样本数据支持公司估计的数据。